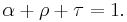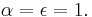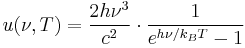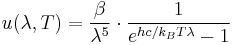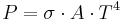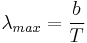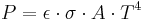Thermal radiation

Thermal radiation is electromagnetic radiation emitted from a material which is due to the heat of the material, the characteristics of which depend on its temperature. An example of thermal radiation is the infrared radiation emitted by a common household radiator or electric heater. A person near a raging bonfire will feel the radiated heat of the fire, even if the surrounding air is very cold. Thermal radiation is generated when heat from the movement of charges in the material (electrons and protons in common forms of matter) is converted to electromagnetic radiation. Sunshine, or solar radiation, is thermal radiation from the extremely hot gases of the Sun, and this radiation heats the Earth. The Earth also emits thermal radiation, but at a much lower intensity because it is cooler. The balance between heating by incoming solar thermal radiation and cooling by the Earth's outgoing thermal radiation is the primary process that determines the Earth's overall temperature.
If the object is a black body in thermodynamic equilibrium, the radiation is termed black-body radiation[1]. The emitted wave frequency of the black body thermal radiation is described by a probability distribution depending only on temperature, and for a genuine black body in thermodynamic equilibrium is given by Planck’s law of radiation. Wien's law gives the most likely frequency of the emitted radiation, and the Stefan–Boltzmann law gives the radiant intensity.[2]
Contents |
Overview
Thermal radiation is the transfer of heat energy through empty space by electromagnetic waves. All objects with a temperature above absolute zero radiate energy at a rate equal to their emissivity multiplied by the rate at which energy would radiate from them if they were a black body. No medium is necessary for radiation to occur, for it is transferred by electromagnetic waves; radiation takes place even in and through a perfect vacuum. For instance, the energy from the Sun travels through the vacuum of space before warming the earth. Radiation is the only form of heat transfer that can occur in the absence of any form of medium (i.e., through a vacuum).
Thermal radiation is a direct result of the movements of atoms and molecules in a material. Since these atoms and molecules are composed of charged particles (protons and electrons), their movements result in the emission of electromagnetic radiation, which carries energy away from the surface. At the same time, the surface is constantly bombarded by radiation from the surroundings, resulting in the transfer of energy to the surface. Since the amount of emitted radiation increases with increasing temperature, a net transfer of energy from higher temperatures to lower temperatures results. Radiation is the only form of heat transfer that can occur in the absence of any form of medium (i.e., through a vacuum).
Both reflectivity and emissivity of all bodies is wavelength dependent. The temperature determines the wavelength distribution of the electromagnetic radiation as limited in intensity by Planck’s law of black-body radiation. For any body the reflectivity depends on the wavelength distribution of incoming electromagnetic radiation and therefore the temperature of the source of the radiation. The emissivity depends on the wave length distribution and therefore the temperature of the body itself. For example, fresh snow, which is highly reflective to visible light, (reflectivity about 0.90) appears white due to reflecting sunlight with a peak energy wavelength of about 0.5 micrometres. Its emissivity, however, at a temperature of about -5°C, peak energy wavelength of about 12 micrometres, is 0.99.
Gases absorb and emit energy in characteristic wavelength patterns that are different for each gas.
Visible light is another form of electromagnetic radiation with a shorter wavelength (and therefore a higher frequency) than infrared radiation. The difference between visible light and the radiation from objects at conventional temperatures is a factor of about 20 in frequency and wavelength; the two kinds of emission are simply different "colors" of electromagnetic radiation.
The power that a black body emits at various frequencies is described by Planck's law. For any given temperature, there is a frequencyfmax at which the power emitted is a maximum. Wien's displacement law, and the fact that the frequency of light is inversely proportional to its wavelength in vacuum, mean that the peak frequency fmax is proportional to the absolute temperature T of the black body. The photosphere of the Sun, at a temperature of approximately 6000 K, emits radiation principally in the visible portion of the spectrum. The Earth's atmosphere is partly transparent to visible light, and the light reaching the Earth's surface is absorbed or reflected. The Earth's surface emits the absorbed radiation, approximating the behavior of a black body at 300 K with spectral peak atfmax. At these lower frequencies, the atmosphere is largely opaque and radiation from the Earth's surface is absorbed or scattered by the atmosphere. Though some radiation escapes into space, it is absorbed and subsequently re-emitted by atmospheric gases. It is this spectral selectivity of the atmosphere that is responsible for the planetary greenhouse effect, contributing to global warming and climate change in general.
The common household lightbulb has a spectrum overlapping the blackbody spectra of the sun and the earth. A portion of the photons emitted by a tungsten light bulb filament at 3000K are in the visible spectrum. However, most of the energy is associated with photons of longer wavelengths; these will not help a person see, but will still transfer heat to the environment, as can be deduced empirically by observing a household incandescent lightbulb. Whenever EM radiation is emitted and then absorbed, heat is transferred. This principle is used inmicrowave ovens, laser cutting, and RF hair removal.
Unlike conductive and convective forms of heat transfer, thermal radiation can be concentrated in a tiny spot by using reflecting mirrors.Concentrating solar power takes advantage of this fact. In many such systems, mirrors are employed to concentrate sunlight into a smaller area. In lieu of mirrors, Fresnel lenses can also be used to concentrate heat flux. Either method can be used to quickly vaporize water into steam using sunlight. For example, the sunlight reflected from mirrors heats the PS10 solar power tower, and during the day it can heat water to 285°C (558.15°K) or 545°F, which exceeds vacuum temperatures experienced by spacecraft in orbit around the Earth.
Surface effects
Lighter colors and also whites and metallic substances absorb less illuminating light, and thus heat up less; but otherwise color makes small difference as regards heat transfer between an object at everyday temperatures and its surroundings, since the dominant emitted wavelengths are nowhere near the visible spectrum, but rather in the far infrared. Emissivities at those wavelengths have little to do with visual emissivities (visible colors); in the far infrared, most objects have high emissivities. Thus, except in sunlight, the color of clothing makes little difference as regards warmth; likewise, paint color of houses makes little difference to warmth except when the painted part is sunlit.
The main exception to this is shiny metal surfaces, which have low emissivities both in the visible wavelengths and in the far infrared. Such surfaces can be used to reduce heat transfer in both directions; an example of this is the multi-layer insulation used to insulate spacecraft.
Low-emissivity windows in houses are a more complicated technology, since they must have low emissivity at thermal wavelengths while remaining transparent to visible light.
Properties
There are four main properties that characterize thermal radiation:
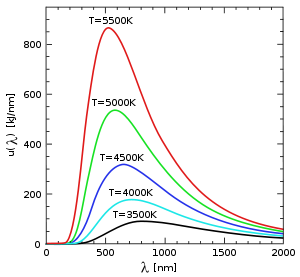
- Thermal radiation, even at a single temperature, occurs at a wide range of frequencies. How much of each frequency is given by Planck’s law of radiation (for idealized materials). This is shown by the curves in the diagram on the right.
- The main frequency (or color) range of the emitted radiation includes higher and higher frequencies as the temperature increases. For example, a red hot object radiates enough in the long wavelengths (red and orange) of the visible band to see, which is why it appears red. If it heats up further, it also begins to emit discernible amounts of green and blue light, and the spread of frequencies mentioned in the first point make it appear white. We then say the object is white hot. However, even at a "white-hot" temperature of 2000 K, 99% of the energy of the radiation is still in the infrared. This is related to Wien's displacement law. In the diagram the peak value for each curve moves to the left as the temperature increases.
- The total amount of radiation, of all frequencies, goes up very fast as the temperature rises (it grows as T4, where T is the absolute temperature of the body). An object at the temperature of a kitchen oven (about twice room temperature in absolute terms: 600 K vs. 300 K) radiates 16 times as much power per unit area. An object at the temperature of the filament in an incandescent bulb (roughly 3000 K, or 10 times room temperature) radiates 10,000 times as much per unit area. The total radiative intensity in a cavity that contains a black body in thermodynamic equilibrium rises as the fourth power of the absolute temperature, the Stefan–Boltzmann law. In the plot, the area under each curve rises rapidly as the temperature increases.
- The rate of thermal radiation of a particular kind of electromagnetic wave is proportional to the amount of absorption that the same type of wave experiences. Thus, a surface that absorbs more red light thermally radiates more red light. This principle applies to all properties of the wave, including wavelength (color), direction, polarization, and even coherence, so that it is quite possible to have thermal radiation which is polarized, coherent, and directional, though polarized and coherent forms are fairly rare in nature.
These properties apply if the distances considered are much larger than the wavelengths contributing to the spectrum (most significant from 8-25 micrometres at 300 K). Indeed, thermal radiation here takes only travelling waves into account. A more sophisticated framework involving electromagnetics has to be used for lower distances (near-field thermal radiation).
| °C | Subjective colour [2] |
|---|---|
| 480 | faint red glow |
| 580 | dark red |
| 730 | bright red, slightly orange |
| 930 | bright orange |
| 1100 | pale yellowish orange |
| 1300 | yellowish white |
| > 1400 | white (yellowish if seen from a distance through atmosphere) |
Interchange of energy
Thermal radiation is an important concept in thermodynamics as it is partially responsible for heat exchange between objects, as warmer bodies radiate more heat than colder ones. (Other factors are convection and conduction.) The interplay of energy exchange is characterized by the following equation:
Here, 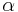 represents spectral absorption factor,
represents spectral absorption factor, 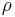 spectral reflection factor and
spectral reflection factor and 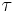 spectral transmission factor. All these elements depend also on the wavelength
spectral transmission factor. All these elements depend also on the wavelength 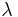 . The spectral absorption factor is equal to the emissivity
. The spectral absorption factor is equal to the emissivity 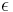 ; this relation is known as Kirchhoff's law of thermal radiation. An object is called a black body if, for all frequencies, the following formula applies:
; this relation is known as Kirchhoff's law of thermal radiation. An object is called a black body if, for all frequencies, the following formula applies:
In a practical situation and room-temperature setting, humans lose considerable energy due to thermal radiation. However, the energy lost by emitting infrared heat is partially regained by absorbing the heat of surrounding objects (the remainder resulting from generated heat through metabolism). Human skin has an emissivity of very close to 1.0 .[3] Using the formulas below then shows a human being, roughly 2 square meter in area, and about 307 kelvins in temperature, continuously radiates about 1000 watts. However, if people are indoors, surrounded by surfaces at 296 K, they receive back about 900 watts from the wall, ceiling, and other surroundings, so the net loss is only about 100 watts. These heat transfer estimates are highly dependent on extrinsic variables, such as wearing clothes (decreasing total thermal "circuit" conductivity, therefore reducing total output heat flux.) Only truly "grey" systems (relative equivalent emissivity/absorptivity and no directional transmissivity dependence in all control volume bodies considered) can achieve reasonable steady-state heat flux estimates through the Stefan-Boltzmann law. Encountering this "ideally calculable" situation is virtually impossible (although common engineering procedures surrender the dependency of these unknown variables and "assume" this to be the case). Optimistically, these "grey" approximations will get you close to real solutions, as most divergence from Stefan-Boltzmann solutions is very small (especially in most STP lab controlled environments).
If objects appear white (reflective in the visual spectrum), they are not necessarily equally reflective (and thus non-emissive) in the thermal infrared; e. g. most household radiators are painted white despite the fact that they have to be good thermal radiators. Acrylic and urethane based white paints have 93% blackbody radiation efficiency at room temperature[4] (meaning the term "black body" does not always correspond to the visually perceived color of an object). These materials that do not follow the "black color = high emissivity/absorptivity" caveat will most likely have functional spectral emissivity/absorptivity dependence.
Calculation of radiative heat transfer between groups of object, including a 'cavity' or 'surroundings' requires solution of a set of simultaneous equations using the Radiosity method. In these calculations, the geometrical configuration of the problem is distilled to a set of numbers called view factors, which give the proportion of radiation leaving any given surface that hits another specific surface. These calculations are important in the fields of solar thermal energy, boiler and furnace design and raytraced computer graphics.
Formula
Thermal radiation power of a black body per unit of solid angle and per unit frequency 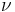 is given by Planck's law as:
is given by Planck's law as:
or
where 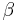 is a constant.
is a constant.
This formula mathematically follows from calculation of spectral distribution of energy in quantized electromagnetic field which is in complete thermal equilibrium with the radiating object.
Integrating the above equation over 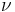 the power output given by the Stefan–Boltzmann law is obtained, as:
the power output given by the Stefan–Boltzmann law is obtained, as:
where the constant of proportionality 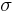 is the Stefan–Boltzmann constant and
is the Stefan–Boltzmann constant and 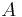 is the radiating surface area.
is the radiating surface area.
Further, the wavelength 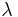 , for which the emission intensity is highest, is given by Wien's Law as:
, for which the emission intensity is highest, is given by Wien's Law as:
For surfaces which are not black bodies, one has to consider the (generally frequency dependent) emissivity factor 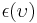 . This factor has to be multiplied with the radiation spectrum formula before integration. If it is taken as a constant, the resulting formula for the power output can be written in a way that contains
. This factor has to be multiplied with the radiation spectrum formula before integration. If it is taken as a constant, the resulting formula for the power output can be written in a way that contains 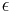 as a factor:
as a factor:
This type of theoretical model, with frequency-independent emissivity lower than that of a perfect black body, is often known as a gray body. For frequency-dependent emissivity, the solution for the integrated power depends on the functional form of the dependence, though in general there is no simple expression for it. Practically speaking, if the emissivity of the body is roughly constant around the peak emission wavelength, the gray body model tends to work fairly well since the weight of the curve around the peak emission tends to dominate the integral.
Constants
Definitions of constants used in the above equations:
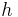 |
Planck's constant | 6.626 0693(11)×10−34 J·s = 4.135 667 43(35)×10−15 eV·s |
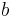 |
Wien's displacement constant | 2.897 7685(51)×10−3 m·K |
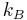 |
Boltzmann constant | 1.380 6505(24)×10−23 J·K−1 = 8.617 343(15)×10−5 eV·K−1 |
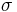 |
Stefan–Boltzmann constant | 5.670 400(40)×10−8 W·m−2·K−4 |
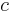 |
Speed of light | 299,792,458 m·s−1 |
Variables
Definitions of variables, with example values:
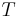 |
Absolute Temperature | For units used above, must be in Kelvin (e.g. Average surface temperature on Earth = 288 K) |
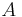 |
Surface area | Acuboid = 2ab + 2bc + 2ac; Acylinder = 2π·r(h + r); Asphere = 4π·r2 |
See also
- Black body
- Incandescence
- Thermography
- Infrared photography
- Planck radiation
- Thermal dose unit
- Color temperature
- Sakuma–Hattori equation
References
- ↑ K. Huang, Statistical Mechanics (2003), p278
- ↑ K. Huang, Statistical Mechanics (2003), p280
- ↑ R. Bowling Barnes (24 May 1963). "Thermography of the Human Body Infrared-radiant energy provides new concepts and instrumentation for medical diagnosis". Science 140 (3569): 870–877. doi:10.1126/science.140.3569.870.
- ↑ S. Tanemura, M. Tazawa, P. Jing, T. Miki, K. Yoshimura, K. Igarashi, M. Ohishi, K. Shimono, M. Adachi, Optical Properties and Radiative Cooling Power of White Paints,[1] ISES 1999 Solar World Congress
Related reading:
- Siegel, John R. Howell, Robert; Howell. John R. (2001-11). Thermal radiation heat transfer. New York: Taylor & Francis, Inc.. pp. (xix - xxvi list of symbols for thermal radiation formulas). ISBN 9781560328391. http://books.google.com/?id=O389yQ0-fecC&pg=PA1&dq=Thermal+radiation. Retrieved 2009-07-23.
External links
- Black Body Emission Calculator
- Free Black Body Emission Calculator (Warning: The Java app at this link crashes Firefox & Netscape)
- Heat Transfer
- Thermal Radiation
- Atmospheric Radiation
- Infrared Temperature Calibration 101
- An Airport-Passenger-Screening System based on Emitted IR and Thermal Radiation
|
||||||||||||||||||||||